Dan’s extended comment about the West Wing poisoning the liberal vision of government also makes me wonder some things. To me, the show tried to portray government as it could be (“with all its failings in the past, and in times to come”), as “an instrument of good”, as a “place where people can come together.” Yes, I’m using quotes from the show to illustrate my points, don’t judge me. Is this not what “liberals” want government to be? Further, regarding the idea that the show portrays the process as being “a group of smart people in a room” and the critique of the complex legislation that came out of the Obama administration, I wonder why we are demonizing complex solutions to complex problems? Is simplicity always the most virtuous option? This question is relevant in government as well as in mathematics, physics, and epidemiology, among others. Does the incessant search for a more “elegant” or “sophisticated” solution leave us disconnected from what is, by all accounts, a highly complex reality? Running a nation of 330 million people is a complex endeavor. So is describing the fundamental mechanisms and evolution of a (potentially) infinite universe over the course of 13 billion years. So is attempting to understand the spread of a novel virus in a human population of 7 billion persons. Simplicity is not our ally in those searches for understanding.
Lastly, is it now true that in order to be an orthodox liberal, I have to allow it to permeate every portion of my life, my intellect, and my personality? Am I only allowed to watch (and want to watch) programming that portrays a world that aligns precisely with the ideals of the liberal movement? To be clear, I know the answer is no, but Dan’s post would seem to imply that my liberalism should stop me from enjoying some damned good (if flawed) television. I should not and will not relinquish my claim to liberalism because I enjoy the West Wing. While clearly it has stopped Dan from enjoying it, and I respect that, I hold no such compunction and no one else should feel that way either.
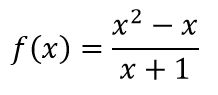

 RSS Feed
RSS Feed